本文目的是搞清楚具有基函数(basis function)情况下，具体的计算细节中是怎么样的。

一维情况

输入输出均为一维向量的情况（一个样本）

Linear regression

一般情况下的线性回归(Linear Rgression)可以表达为：

${y}(\bf {x},\bf {w}$$) = w_0 + \sum_i^N{w_ix_i}$

其中$\bf x$ $= [x_1,x_2,…,x_n]^T$。

多项式基函数下的线性回归(Linear Regression)可以表达为：

设数据集为$\bf x = [x_1,x_2,…,x_n]$， $\bf y = [y_1,y1,…,y_n]$。$\bf x$，$\bf y$构成一条曲线。现由$M-1$个多项式去拟合该曲线。

$y_n = w_0 + \sum_j^{M-1}{\phi _j(x_n)}$

其中$\phi_j(x) = x^j$

多项式中，对于某个数据点$x_n$，由$\phi_1(x_n) = x_n^1, \phi_2(x_n) = x_n^2,…, \phi_{M-1}(x_n) = x_n^{M-1}$这些基函数的线性组合成$y_n$。

高斯基函数有以下形式：

$\phi_j(x) = exp(-\frac {(x-\mu_j)^2}{2s^2})$

上式中$\mu_j$和$s$该如何确定呢？

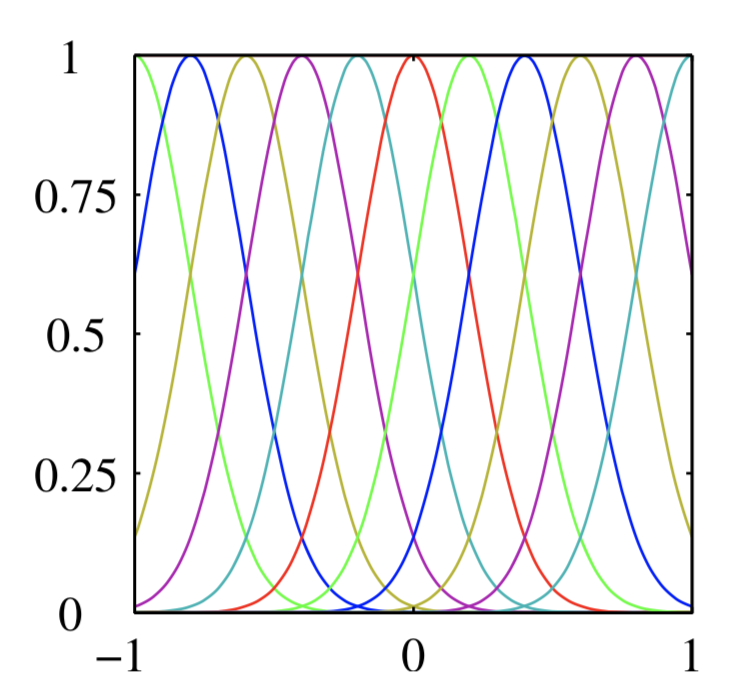Gaussian basis function

$s$是需要自己调整的，而$\mu_j$的则在间距为$s$的网格上。

Like this:

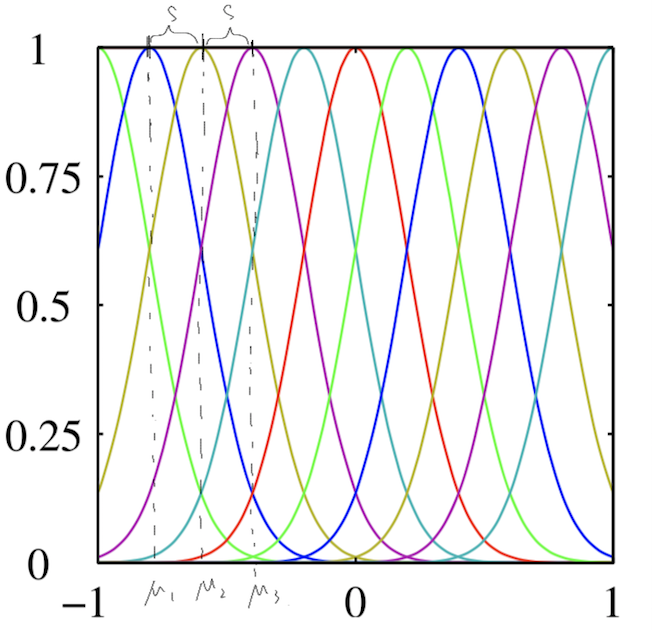$\mu$ and $s$

Different $s$